3 - Optimised Sensor Management

This tutorial follows on from the Multi Sensor Management tutorial and explores the use of external optimisation libraries to overcome the limitations of the brute force optimisation method introduced in the previous tutorial.

The scenario in this example is the same as Tutorial 2, simulating 3 targets moving on nearly constant velocity trajectories and an adjustable number of sensors. The sensors are RadarRotatingBearingRange with a defined field of view which can be pointed in a particular direction in order to make an observation.

The optimised sensor managers are built around the SciPy optimize library. Similar to the brute force method introduced previously the sensor manager considers all possible configurations of sensors and actions and here uses an optimising function to optimise over a given reward function, returning the optimal configuration.

The UncertaintyRewardFunction is used for all sensor managers which chooses the configuration for which the sum of estimated uncertainties (as represented by the Frobenius norm of the covariance matrix) can be reduced the most by using the chosen sensing configuration.

As in the previous tutorials the SIAP 1 and uncertainty metrics are used to assess the performance of the sensor managers.

Sensor Management example

Setup

First a simulation must be set up using components from Stone Soup. For this the following imports are required.

import numpy as np
import random
from datetime import datetime, timedelta

start_time = datetime.now()

from stonesoup.models.transition.linear import CombinedLinearGaussianTransitionModel, ConstantVelocity
from stonesoup.types.groundtruth import GroundTruthPath, GroundTruthState

Generate ground truths

Generate transition model and ground truths as in Tutorials 1 & 2.

The number of targets in this simulation is defined by ntruths - here there are 3 targets travelling in different directions. The time the simulation is observed for is defined by time_max.

We can fix our random number generator in order to probe a particular example repeatedly. This can be undone by commenting out the first two lines in the next cell.

np.random.seed(1990)
random.seed(1990)

# Generate transition model
transition_model = CombinedLinearGaussianTransitionModel([ConstantVelocity(0.005),
                                                          ConstantVelocity(0.005)])

yps = range(0, 100, 10)  # y value for prior state
truths = []
ntruths = 3  # number of ground truths in simulation
time_max = 50  # timestamps the simulation is observed over

xdirection = 1
ydirection = 1

# Generate ground truths
for j in range(0, ntruths):
    truth = GroundTruthPath([GroundTruthState([0, xdirection, yps[j], ydirection], timestamp=start_time)],
                            id=f"id{j}")

    for k in range(1, time_max):
        truth.append(
            GroundTruthState(transition_model.function(truth[k - 1], noise=True, time_interval=timedelta(seconds=1)),
                             timestamp=start_time + timedelta(seconds=k)))
    truths.append(truth)

    xdirection *= -1
    if j % 2 == 0:
        ydirection *= -1

Plot the ground truths. This is done using the Plotterly class from Stone Soup.

from stonesoup.plotter import Plotterly

# Stonesoup plotter requires sets not lists
truths_set = set(truths)

plotter = Plotterly()
plotter.plot_ground_truths(truths_set, [0, 2])
plotter.fig

Create sensors

Create a set of sensors for each sensor management algorithm. As in Tutorial 2 this tutorial uses the RadarRotatingBearingRange sensor with the number of sensors initially set as 2 and each sensor positioned along the line \(x=10\), at distance intervals of 50.

total_no_sensors = 2

from stonesoup.types.state import StateVector
from stonesoup.sensor.radar.radar import RadarRotatingBearingRange
from stonesoup.types.angle import Angle

sensor_setA = set()
for n in range(0, total_no_sensors):
    sensor = RadarRotatingBearingRange(
        position_mapping=(0, 2),
        noise_covar=np.array([[np.radians(0.5) ** 2, 0],
                              [0, 1 ** 2]]),
        ndim_state=4,
        position=np.array([[10], [n * 50]]),
        rpm=60,
        fov_angle=np.radians(30),
        dwell_centre=StateVector([0.0]),
        max_range=np.inf,
        resolutions={'dwell_centre': Angle(np.radians(30))}
    )
    sensor_setA.add(sensor)
for sensor in sensor_setA:
    sensor.timestamp = start_time

sensor_setB = set()
for n in range(0, total_no_sensors):
    sensor = RadarRotatingBearingRange(
        position_mapping=(0, 2),
        noise_covar=np.array([[np.radians(0.5) ** 2, 0],
                              [0, 1 ** 2]]),
        ndim_state=4,
        position=np.array([[10], [n * 50]]),
        rpm=60,
        fov_angle=np.radians(30),
        dwell_centre=StateVector([0.0]),
        max_range=np.inf,
        resolutions={'dwell_centre': Angle(np.radians(30))}
    )
    sensor_setB.add(sensor)

for sensor in sensor_setB:
    sensor.timestamp = start_time

sensor_setC = set()
for n in range(0, total_no_sensors):
    sensor = RadarRotatingBearingRange(
        position_mapping=(0, 2),
        noise_covar=np.array([[np.radians(0.5) ** 2, 0],
                              [0, 1 ** 2]]),
        ndim_state=4,
        position=np.array([[10], [n * 50]]),
        rpm=60,
        fov_angle=np.radians(30),
        dwell_centre=StateVector([0.0]),
        max_range=np.inf,
        resolutions={'dwell_centre': Angle(np.radians(30))}
    )
    sensor_setC.add(sensor)

for sensor in sensor_setC:
    sensor.timestamp = start_time

Create the Kalman predictor and updater

Construct a predictor and updater using the KalmanPredictor and ExtendedKalmanUpdater components from Stone Soup. The measurement model for the updater is None as it is an attribute of the sensor.

from stonesoup.predictor.kalman import KalmanPredictor
predictor = KalmanPredictor(transition_model)

from stonesoup.updater.kalman import ExtendedKalmanUpdater
updater = ExtendedKalmanUpdater(measurement_model=None)
# measurement model is added to detections by the sensor

Run the Kalman filters

Create priors which estimate the targets’ initial states - these are the same as in the previous sensor management tutorials.

from stonesoup.types.state import GaussianState

priors = []
xdirection = 1.2
ydirection = 1.2
for j in range(0, ntruths):
    priors.append(GaussianState([[0], [xdirection], [yps[j]+0.1], [ydirection]],
                                np.diag([0.5, 0.5, 0.5, 0.5]+np.random.normal(0,5e-4,4)),
                                timestamp=start_time))
    xdirection *= -1
    if j % 2 == 0:
        ydirection *= -1

Initialise the tracks by creating an empty list and appending the priors generated. This needs to be done separately for each sensor manager method as they will generate different sets of tracks.

from stonesoup.types.track import Track

# Initialise tracks from the BruteForceSensorManager
tracksA = []
for j, prior in enumerate(priors):
    tracksA.append(Track([prior]))

# Initialise tracks from the OptimizeBruteSensorManager
tracksB = []
for j, prior in enumerate(priors):
    tracksB.append(Track([prior]))

# Initialise tracks from the OptimizeBasinHoppingSensorManager
tracksC = []
for j, prior in enumerate(priors):
    tracksC.append(Track([prior]))

Create sensor managers

The UncertaintyRewardFunction will be used for each sensor manager as in Tutorials 1 & 2 and the BruteForceSensorManager will be used as a comparison to the optimised methods.

from stonesoup.sensormanager.reward import UncertaintyRewardFunction
from stonesoup.sensormanager import BruteForceSensorManager

Optimised Brute Force Sensor Manager

The first optimised method, OptimizeBruteSensorManager uses brute() which minimizes a function over a given range using a brute force method. This can be tailored by setting the number of grid points to search over or by adding the use of a polishing function.

from stonesoup.sensormanager import OptimizeBruteSensorManager

Optimised Basin Hopping Sensor Manager

The second optimised method, OptimizeBasinHoppingSensorManager uses basinhopping() which finds the global minimum of a function using the basin-hopping algorithm. This is a combination of a global stepping algorithm and local minimization at each step. Parameters such as number of basin hopping iterations or stepsize can be set to tailor the algorithm to requirements.

from stonesoup.sensormanager import OptimizeBasinHoppingSensorManager

Initiate sensor managers

Create an instance of each sensor manager class. For the optimised sensor managers the default settings will be used meaning only a sensor set and reward function is required. The UncertaintyRewardFunction will be used for each sensor manager. For the OptimizeBruteSensorManager a polishing function is used by setting finish=True.

# initiate reward function
reward_function = UncertaintyRewardFunction(predictor, updater)

bruteforcesensormanager = BruteForceSensorManager(sensor_setA,
                                                  reward_function=reward_function)

optimizebrutesensormanager = OptimizeBruteSensorManager(sensor_setB,
                                                        reward_function=reward_function,
                                                        finish=True)

optimizebasinhoppingsensormanager = OptimizeBasinHoppingSensorManager(sensor_setC,
                                                                      reward_function=reward_function)

Run the sensor managers

Each sensor management method requires a timestamp and a list of tracks at each time step when calling the function choose_actions(). This returns a mapping of sensors and actions to be taken by each sensor, decided by the sensor managers.

For each sensor management method, at each time step the chosen action is given to the sensors and then measurements taken. At each timestep the tracks are predicted and those with measurements associated are updated.

First a hypothesiser and data associator are required for use in each tracker.

from stonesoup.hypothesiser.distance import DistanceHypothesiser
from stonesoup.measures import Mahalanobis
hypothesiser = DistanceHypothesiser(predictor, updater, measure=Mahalanobis(), missed_distance=5)

from stonesoup.dataassociator.neighbour import GNNWith2DAssignment
data_associator = GNNWith2DAssignment(hypothesiser)

Run brute force sensor manager

Each sensor manager is run in the same way as in the previous tutorials.

from ordered_set import OrderedSet
import time

# Start timer for cell execution time
cell_start_time1 = time.time()

# Generate list of timesteps from ground truth timestamps
timesteps = []
for state in truths[0]:
    timesteps.append(state.timestamp)

for timestep in timesteps[1:]:

    # Generate chosen configuration
    chosen_actions = bruteforcesensormanager.choose_actions(tracksA, timestep)

    # Create empty dictionary for measurements
    measurementsA = []

    for chosen_action in chosen_actions:
        for sensor, actions in chosen_action.items():
            sensor.add_actions(actions)

    for sensor in sensor_setA:
        sensor.act(timestep)

        # Observe this ground truth
        measurements = sensor.measure(OrderedSet(truth[timestep] for truth in truths), noise=True)
        measurementsA.extend(measurements)

    hypotheses = data_associator.associate(tracksA,
                                           measurementsA,
                                           timestep)
    for track in tracksA:
        hypothesis = hypotheses[track]
        if hypothesis.measurement:
            post = updater.update(hypothesis)
            track.append(post)
        else:  # When data associator says no detections are good enough, we'll keep the prediction
            track.append(hypothesis.prediction)

cell_run_time1 = round(time.time() - cell_start_time1, 2)

Plot ground truths, tracks and uncertainty ellipses for each target. The positions of the sensors are indicated by black x markers.

plotterA = Plotterly()
plotterA.plot_sensors(sensor_setA)
plotterA.plot_ground_truths(truths_set, [0, 2])
plotterA.plot_tracks(set(tracksA), [0, 2], uncertainty=True)
plotterA.fig

The resulting plot is exactly the same as Tutorial 2.

Run optimised brute force sensor manager

# Start timer for cell execution time
cell_start_time2 = time.time()

for timestep in timesteps[1:]:

    # Generate chosen configuration
    chosen_actions = optimizebrutesensormanager.choose_actions(tracksB, timestep)

    # Create empty dictionary for measurements
    measurementsB = []

    for chosen_action in chosen_actions:
        for sensor, actions in chosen_action.items():
            sensor.add_actions(actions)

    for sensor in sensor_setB:
        sensor.act(timestep)

        # Observe this ground truth
        measurements = sensor.measure(OrderedSet(truth[timestep] for truth in truths), noise=True)
        measurementsB.extend(measurements)

    hypotheses = data_associator.associate(tracksB,
                                           measurementsB,
                                           timestep)
    for track in tracksB:
        hypothesis = hypotheses[track]
        if hypothesis.measurement:
            post = updater.update(hypothesis)
            track.append(post)
        else:  # When data associator says no detections are good enough, we'll keep the prediction
            track.append(hypothesis.prediction)

cell_run_time2 = round(time.time() - cell_start_time2, 2)

Plot ground truths, tracks and uncertainty ellipses for each target.

plotterB = Plotterly()
plotterB.plot_sensors(sensor_setB)
plotterB.plot_ground_truths(truths_set, [0, 2])
plotterB.plot_tracks(set(tracksB), [0, 2], uncertainty=True)
plotterB.fig

Run optimised basin hopping sensor manager

# Start timer for cell execution time
cell_start_time3 = time.time()

for timestep in timesteps[1:]:

    # Generate chosen configuration
    chosen_actions = optimizebasinhoppingsensormanager.choose_actions(tracksC, timestep)

    # Create empty dictionary for measurements
    measurementsC = []

    for chosen_action in chosen_actions:
        for sensor, actions in chosen_action.items():
            sensor.add_actions(actions)

    for sensor in sensor_setC:
        sensor.act(timestep)

        # Observe this ground truth
        measurements = sensor.measure(OrderedSet(truth[timestep] for truth in truths), noise=True)
        measurementsC.extend(measurements)

    hypotheses = data_associator.associate(tracksC,
                                           measurementsC,
                                           timestep)
    for track in tracksC:
        hypothesis = hypotheses[track]
        if hypothesis.measurement:
            post = updater.update(hypothesis)
            track.append(post)
        else:  # When data associator says no detections are good enough, we'll keep the prediction
            track.append(hypothesis.prediction)

cell_run_time3 = round(time.time() - cell_start_time3, 2)

Plot ground truths, tracks and uncertainty ellipses for each target.

plotterC = Plotterly()
plotterC.plot_sensors(sensor_setC)
plotterC.plot_ground_truths(truths_set, [0, 2])
plotterC.plot_tracks(set(tracksC), [0, 2], uncertainty=True)
plotterC.fig

At first glance, the plots for each of the optimised sensor managers show a very similar tracking performance to the BruteForceSensorManager.

Metrics

As in Tutorials 1 & 2 the SIAP and uncertainty metrics are used to compare the tracking performance of the sensor managers in more detail.

from stonesoup.metricgenerator.tracktotruthmetrics import SIAPMetrics
from stonesoup.measures import Euclidean
siap_generator = SIAPMetrics(position_measure=Euclidean((0, 2)),
                             velocity_measure=Euclidean((1, 3)))

from stonesoup.dataassociator.tracktotrack import TrackToTruth
associator = TrackToTruth(association_threshold=30)

from stonesoup.metricgenerator.uncertaintymetric import SumofCovarianceNormsMetric
uncertainty_generator = SumofCovarianceNormsMetric()

Generate a metric manager for each sensor management method.

from stonesoup.metricgenerator.manager import SimpleManager

metric_managerA = SimpleManager([siap_generator, uncertainty_generator],
                                associator=associator)

metric_managerB = SimpleManager([siap_generator, uncertainty_generator],
                                associator=associator)

metric_managerC = SimpleManager([siap_generator, uncertainty_generator],
                                associator=associator)

For each time step, data is added to the metric manager on truths and tracks. The metrics themselves can then be generated from the metric manager.

metric_managerA.add_data(truths, tracksA)
metric_managerB.add_data(truths, tracksB)
metric_managerC.add_data(truths, tracksC)

metricsA = metric_managerA.generate_metrics()
metricsB = metric_managerB.generate_metrics()
metricsC = metric_managerC.generate_metrics()

SIAP metrics

First we look at SIAP metrics. We are only interested in the positional accuracy (PA) and velocity accuracy (VA). These metrics can be plotted to show how they change over time.

import matplotlib.pyplot as plt

fig, axes = plt.subplots(2)

times = metric_managerA.list_timestamps()

pa_metricA = metricsA['SIAP Position Accuracy at times']
va_metricA = metricsA['SIAP Velocity Accuracy at times']

pa_metricB = metricsB['SIAP Position Accuracy at times']
va_metricB = metricsB['SIAP Velocity Accuracy at times']

pa_metricC = metricsC['SIAP Position Accuracy at times']
va_metricC = metricsC['SIAP Velocity Accuracy at times']

axes[0].set(title='Positional Accuracy', xlabel='Time', ylabel='PA')
axes[0].plot(times, [metric.value for metric in pa_metricA.value],
             label='BruteForceSensorManager')
axes[0].plot(times, [metric.value for metric in pa_metricB.value],
             label='OptimizeBruteSensorManager')
axes[0].plot(times, [metric.value for metric in pa_metricC.value],
             label='OptimizeBasinHoppingSensorManager')
axes[0].legend()

axes[1].set(title='Velocity Accuracy', xlabel='Time', ylabel='VA')
axes[1].plot(times, [metric.value for metric in va_metricA.value],
             label='BruteForceSensorManager')
axes[1].plot(times, [metric.value for metric in va_metricB.value],
             label='OptimizeBruteSensorManager')
axes[1].plot(times, [metric.value for metric in va_metricC.value],
             label='OptimizeBasinHoppingSensorManager')
axes[1].legend()

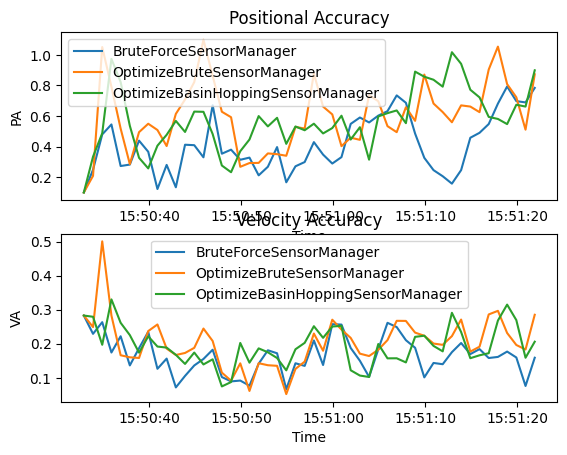
Both graphs show that there is little performance difference between the different sensor managers. Positional accuracy remains consistently good and velocity accuracy improves after overcoming the initial differences in the priors.

Uncertainty metric

Next we look at the uncertainty metric which computes the sum of covariance matrix norms of each state at each time step. This is plotted over time for each sensor manager method.

uncertainty_metricA = metricsA['Sum of Covariance Norms Metric']
uncertainty_metricB = metricsB['Sum of Covariance Norms Metric']
uncertainty_metricC = metricsC['Sum of Covariance Norms Metric']

fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)
ax.plot([i.timestamp for i in uncertainty_metricA.value],
        [i.value for i in uncertainty_metricA.value],
        label='BruteForceSensorManager')
ax.plot([i.timestamp for i in uncertainty_metricB.value],
        [i.value for i in uncertainty_metricB.value],
        label='OptimizeBruteSensorManager')
ax.plot([i.timestamp for i in uncertainty_metricC.value],
        [i.value for i in uncertainty_metricC.value],
        label='OptimizeBasinHoppingSensorManager')
ax.set_ylabel("Sum of covariance matrix norms")
ax.set_xlabel("Time")
ax.legend()

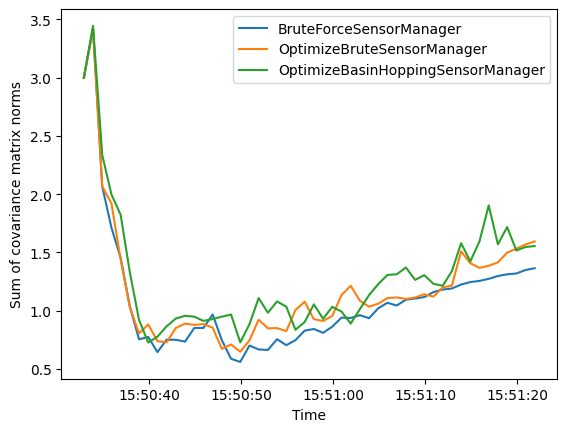
The uncertainty metric shows some variation between the sensor management methods, with a little more variation in the basin hopping method than the brute force methods. Overall they have a similar performance, improving after overcoming the initial differences in the priors.

Cell runtime

Now let us compare the calculated runtime of the tracking loop for each of the sensor managers.

fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)
ax.set_ylabel('Cell run time (s)')
ax.bar(['Brute Force', 'Optimised Brute Force', 'Optimised Basin Hopping'],
       [cell_run_time1, cell_run_time2, cell_run_time3],
       color=['tab:blue', 'tab:orange', 'tab:green'])

print(f'Brute Force: {cell_run_time1} s')
print(f'Optimised Brute Force: {cell_run_time2} s')
print(f'Optimised Basin Hopping: {cell_run_time3} s')

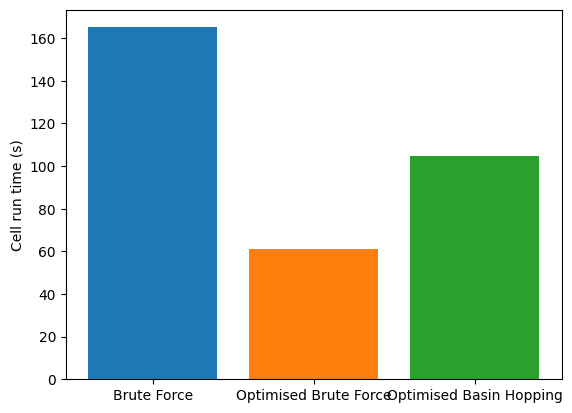
Brute Force: 165.11 s
Optimised Brute Force: 61.3 s
Optimised Basin Hopping: 104.64 s

These run times show that each of the optimised methods are significantly quicker than the brute force method whilst maintaining a similar tracking performance. This difference becomes more clear when the complexity of the situation increases - by including additional sensors for example.

References

1

Votruba, Paul & Nisley, Rich & Rothrock, Ron and Zombro, Brett., Single Integrated Air Picture (SIAP) Metrics Implementation, 2001